Snell's law is a law that describes the passage of light through two nearby media. It is also known as the law of refraction.
n1×Sinθ1=n2×Sinθ2
Sine (sin) is a conversion code for signifying the height of a right triangle using an angle.
Special cases … sin0° = 0, sin30° = 1/2, sin45° = √2/2, sin60° = √3/2, sin90° = 1
As θ increases, sinθ also increases.
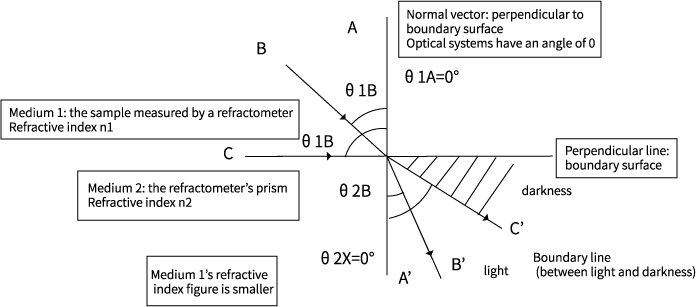
Consider ray A.
θ1A is 0, so regardless of the value of n1, it will come out to 0. To make n2×sinθ2A' equal 0, θ2A' must also be 0. Therefore light that enters from directly above will exit directly below. Normal vector light exits as a normal vector.
BConsider ray B.
n1Sinθ1B=n2Sinθ2B'
Given that n2 is larger than n1, sinθ2B' has to be smaller than sinθ1B or the two sides of the equation will not be equal. To make sinθ smaller, θ must be small, and θ2B' will be a smaller angle of incidence than θ1B. Oblique rays of light like ray B refract and enter the next medium.
Consider ray C.
Ray C is a ray of light at a 90° from the normal vector and is at the boundary surface between the two media.
What is happening to the light at the boundary surface is often unknown, but at least the 89.9 ° ray exists. Light with an angle greater than 90° (90.000001°) is the light from medium 2, so if this light is ignored, a ray with an angle of 90° is the greatest possible angle.
By using sin90° = 1, the multiplication by 1 disappears. The left side of the formula becomes just n1.
n2 is the refractive index of the prism … which is already known.
θ2 is the angle of refraction … which requires n1 to be measured.
Refractive index can be measured by measuring the angle of emergence of light with an angle of incidence of 90° (perpendicular to the prism).
A refractometers is an apparatus that measures the angle of light and converts that angle into the refractive index.

